Kerr-Schild Double Copy and Complex Worldlines

The Schwarzschild black hole is “like” a point charge. It’s a mass localized at the origin which sources a field (\(h_{\mu\nu} \equiv g_{\mu\nu}-\eta_{\mu\nu}\)) which decays as \(\frac{1}{r}\), just like a point charge is a charge localized at the origin which sources a field (\(A_\mu\)) which decays as \(\frac{1}{r}\). Is there a precise way in which these two objects are related? In fact, yes: in 2014, Monteiro et al. presented the Kerr-Schild double copy, which provides a prescription for taking certain stationary solutions to the Einstein equations and writing them as “squares” of solutions to the Maxwell equations.

It’s a simple but brilliant setup, starting with a special class of metrics which have been known since the 1970s, the Kerr-Schild metrics. These are metrics of the form \(g_{\mu\nu} = \eta_{\mu\nu} + \phi k_\mu k_\nu\), where \(\phi\) is some scalar function and \(k_{\mu}\) is a null vector. Null with respect to what metric, you might ask: the background \(\eta_{\mu\nu}\), or the full metric \(g_{\mu\nu}\)? It turns out that it doesn’t matter, you can check that each nullity condition implies the other. The Kerr-Schild metrics form a large class, containing in particular both the Schwarzschild and the Kerr metrics. For the Schwarzschild metric, take spherical coordinates and choose

\[\phi = \frac{r_s}{r},\qquad k^\mu = (\partial_t+\partial_r)^\mu,\]

where \(r_s\) is the Schwarzschild radius. This would be easy enough to come up with by tinkering with the usual Schwarzschild coordinates. For the Kerr metric, take Boyer-Lindquist coordinates and set

\[\phi = \frac{r_s r}{r^2+a^2\cos^2\theta},\qquad k^\mu = \left(\partial_t + \partial_r - \frac{a}{r^2+a^2}\partial_\varphi\right)^\mu.\]

It would be a lot harder to come up with this from scratch, but later we’ll see a slick way to derive it.

Kerr-Schild metrics are most interesting when \(k^\mu\) is a geodesic vector field (which is true for both the Schwarzschild and Kerr solutions above, in particular). For a Kerr-Schild metric with geodesic \(k^\mu\), the Einstein equations become linear in \(\phi\), which is surprising and very cool. Concretely, the Einstein equation reduced to

\[\nabla_\sigma\left(\nabla^\alpha\left(\phi k^\sigma k_\beta\right) + \nabla_\beta\left(\phi k^\sigma k^\alpha\right) - \nabla^\sigma\left(\phi k^\alpha k_\beta\right)\right) = 0.\]

But wait, it gets better. If we assume the metric is stationary – that is, \(\nabla_0\left(\phi k^\mu k^\nu\right) = 0\) – and if we fix \(k_0 = 1\) by appropriately rescaling \(\phi\) – and if we look only at the \(\beta = 0\) components of the Einstein equation above – then this reduces all the way to

\[\nabla_\sigma\left(\nabla^\alpha (\phi k^\sigma) - \nabla^\sigma(\phi k^\alpha)\right) = 0.\]

This is nothing but the Maxwell equations, with \(A^\mu = \phi k^\mu\)! So, sort of incredibly, a Maxwell solution is sitting inside every stationary Kerr-Schild Einstein solution. This is the essense of the Monteiro et al. paper.

So, we had some constraints on \(k^\mu\): it has to be geodesic and null. And now we have a gauge field \(A^\mu = \phi k^\mu\), which as a consequence must also be geodesic and null:

\[A^\mu A_\mu = 0, \qquad A^\mu \nabla_\mu A^\nu = \chi A^\nu,\]

where \(\chi\) is some scalar function (since \(A^\mu\) need not be an affinely parameterized geodesic). Now, a bit of fancy footwork:

\[\chi A^\nu = A^\mu \nabla_\mu A^\nu = A^\mu ({F_\mu}^\nu + \nabla^\nu A_\mu) = -{F^\nu}_\mu A^\mu + \frac{1}{2}\nabla^\nu\left(A^\mu A_\mu\right) = -{F^\nu}_\mu A^\mu.\]

So in fact, the gauge field is an eigenvector of its own field strength. In particular, the field strength has an eigenvector which is null and geodesic (and also shear-free, by the Goldberg-Sachs theorem). Wouldn’t it be nice if someone had classified the Maxwell fields whose field strengths possess such an eigenvector? Well, lucky for us, Ezra Newman did just that. Better yet, he classified these fields in a physically interesting way. When the eigenvector is also non-twisting, then the Maxwell fields of interest are simply the Liénard-Wiechert fields of charges moving along real worldlines. By real worldlines, I mean worldlines with real coordinates, because things get really interesting when the eigenvector has nonzero twist. In that case, Newman’s theorem says that the Maxwell fields are also Liénard-Wiechert fields, but of charges moving on complex worldines.

What does that mean exactly? Well, first, let’s recall the construction of Liénard-Wiechert fields without any of the complex business. Suppose we have a charge \(q\) moving on a worldline \(y^\mu(\tau)\). At some spacetime point \(x^\mu\), the field can only depend on points in its past lightcone, and it’s easy to prove that the intersection of the past lightcone with a worldline is a single point, which we’ll call \(y^\mu\left(\tau_\text{ret}\right)\). Let \(\lambda^\mu\left(\tau_\text{ret}\right) = \left.\frac{dy^\mu}{d\tau}\right\vert_{\tau_\text{ret}}\) be the worldline velocity at that point. Since \(x^\mu - y^\mu\left(\tau_\text{ret}\right)\) is null by construction, we can get the spatial distance to \(x^\mu\) in the frame of the particle using

\[r = \lambda^\mu\left(\tau_\text{ret}\right)\left(x^\mu - y^\mu\left(\tau_\text{ret}\right)\right).\]

With these ingredients we can write the Liénard-Wiechert field. In the instantaneous frame of the particle it should coincide with the Coulomb field, and this suggests

\[A^\mu = \frac{gq}{4\pi r}\lambda^\mu\left(\tau_\text{ret}\right).\label{lw_A}\]

Great. So, what if we allow \(y^\mu(\tau)\) to take complex values – that is, allow the particle to move through a space with 4 complex dimensions, or 8 real dimensions? Then we can follow the same approach, using \eqref{lw_A}, but now \(r\) and \(\lambda^\mu\) can be complex, and we’ll have a complex gauge field, from which we can form a complex field strength. There is a general prescription for taking a complex field strength and building a real field strength from it, which you can find in our paper – but it’s especially easy when the particle isn’t moving, in which case we have just a complex electric field \(\tilde E\). In this case, we let \(E = \text{Re}\,\tilde E\) and \(B = \text{Im}\,\tilde E\), and voilà, we have a real Maxwell field. This approach actually goes all the way back to Riemann.

So now let’s get back to the black hole story. We’ve argued that the gauge fields arising as single copies of Einstein metrics have to be the Liénard-Wiechert fields of charges on complex worldlines. Let’s start with the simplest complex worldline, a charge which just sits at the origin. Of course, this is the Coulomb solution, with

\[A^\mu = \frac{gq}{4\pi r}(\partial_t+\partial_r)^\mu.\]

(Note we have chosen a gauge in which \(A^\mu\) is null – this is not a gauge-invariant condition.) Everything is real already, so no need to worry about imaginary parts. Now let’s see if we can lift it to a metric. We know that \(A^\mu = \phi k^\mu\), so the metric can be written as

\[g_{\mu\nu} = \eta_{\mu\nu} + \phi^{-1}A_\mu A_\nu.\]

We need some criterion for choosing a function \(\phi\). We could use the condition \(k_0 = 1\) from Monteiro et al., in which case we recover the Schwarzschild solution on the nose. More generally, we could look for a \(\phi\) for which the stress tensor is traceless, so that it can be interpreted as a Maxwell stress tensor – and if we do this, we find a \(\phi\) which gives the Reissner-Nördstrom solution.

It gets even better when we go to a charge on a stationary worldline sitting at a complex coordinate. Let the charge be at \(-i\vec{a}\) (where \(\vec{a}\) is a real 3-vector). Then in \eqref{lw_A}, the denominator is \(\vert\vec{x}+i\vec{a}\vert = \sqrt{\vec{x}^2-\vec{a}^2 + 2i\vec{x}\cdot\vec{a}}\). Now, without loss of generality, let \(\vec{a} = a\hat{z}\). If we make a judicious choice of coordinates, namely spheroidal coordinates with

\[x = \sqrt{r^2+a^2}\sin\theta\cos\phi, \qquad y = \sqrt{r^2 + a^2}\sin\theta\sin\phi, \qquad z = r\cos\theta,\]

then we have \(\vert\vec{x}+i\vec{a}\vert = \sqrt{r^2 - a^2\cos^2\theta + 2ira\cos\theta} = r+ia\cos\theta\). Pretty nice! So then,

\[\frac{1}{|\vec{x}+i\vec{a}|} = \frac{r}{r^2+a^2\cos^2\theta} -i\frac{a\cos\theta}{r^2+a^2\cos^2\theta}.\]

Now remember, when we have a complex electric field and no magnetic field, we’re supposed to let the real part be the real electric field adn the imaginary part be the real magnetic field. We can do that, and get a field strength tensor, and then compute its eigenvectors. And lo and behold, those eigenvectors come out to be \(\partial_t \pm \partial_r - \frac{a}{r^2+a^2}\partial_\varphi\), one of which is precisely what we introduced as the Kerr-Schild vector for the Kerr metric in the beginning (and the other one would work just as well). So by shifting a point charge into a complex space, we’ve uncovered the rotating Kerr solution!

Better yet, we can go through the same mechanics as before, choosing a \(\phi\) to go along with our \(k^\mu\) such that the stress tensor is traceless, and we find the charged Kerr-Newman solution. So just like that, we’ve found all the black hole solutions to the Einstein equations in four dimensions. The mass and charge are integration constants, and the spin, in a fascinating turn of events, turned out to be a complex coordinate of a stationary point charge.

It would certainly be nice to carry this story to higher dimensions, but it doesn’t easily translate. Newman’s theorem relies on some particularities of four-dimensional geometry. Indeed, even the ability to identify the position \(\vec{a}\) with an angular momentum breaks down in higher dimensions; the Myers-Perry rotating solution is specified by \(\left\lfloor \frac{D-1}{2}\right\rfloor\) angular momenta in \(D\) spacetime dimensions (the number of independent rotation planes). There may well be a similarly interesting story in higher dimensions, but it’s not a direct corollary of the four-dimensional result presented here.

Nonetheless, there is one thing we can say in general: if a metric can be written in stationary Kerr-Schild coordinates, then it will have a single-copy field strength with a null and geodesic eigenvector. This can be used to furnish a test for “Kerr-Schild-ness.” In our paper, we show how to form a single-copy current out of the Einstein stress tensor in a covariant way, so as long as we know the source of a metric we can extract a corresponding \(j^\mu\) and integrate to find a gauge field and a field strength \({F^\mu}_\nu\). We can then compute the eigenvectors of this field strength and see if they assemble into a null geodesic field.

This works, and it’s a useful test – everything is gauge-invariant (we start with a metric in general coordinates, and end up with a field strength tensor), and at the end we have a fairly stringent test on whether Kerr-Schild coordinates for the metric exist. We can even make the test a bit more physical. Instead of diagonalizing \({F_\mu}^\nu\) everywhere, just do so at a handful of points; use the eigenvectors as initial velocities for charged particles at those points. Then let the particles move under the influence of the Maxwell field. Their trajectories will be tangent to the eigenvectors of \({F_\mu}^\nu\), and so the condition is that these particles move along background geodesics.

As a sanity check, let’s try this for the Kerr metric. We use the Kerr source to find a gauge source, which ends up being a disk of circulating current. We then solve Maxwell’s equations for that source, and find eigenvectors of the field strength at a few points, then use the field strength to evolve our hypothetical particles through time. The result is below. Indeed, we find straight-line trajectories.

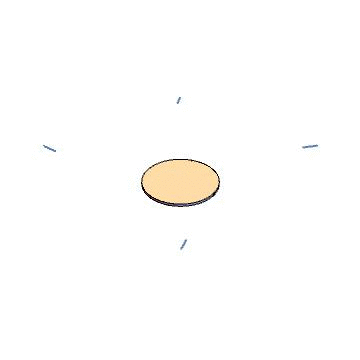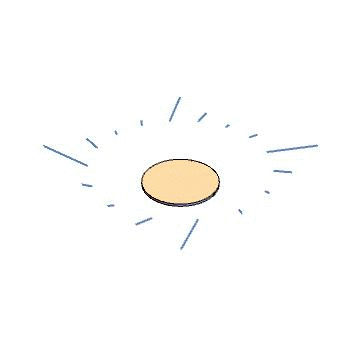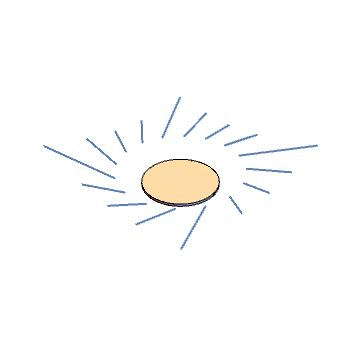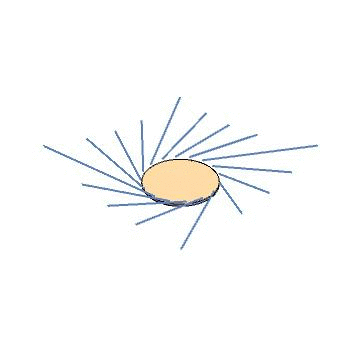
Now for a fancier example. The black ring is a solution to the Einstein equations in five dimensions, with a nontrivial horizon topology (\(S^1\times S^2\)). It is known based on algebraic properties of the Weyl tensor that this metric does not admit Kerr-Schild coordinates. We can use our approach to see this in a more physical way. We follow the same procedure as before – find the source, convert to a gauge source, integrate Maxwell’s equations, diagonalize the field strength tensor, animate some particles – and find the result below. Indeed, the particles are scattered as they pass through the ring source, providing a proof-by-picture that the black ring does not admit Kerr-Schild coordinates.

There’s tons more to explore here. There’s a new way of formulating the double copy, based on curvatures rather than fields. An alternative interpretation of the complex-coordinates approach to the Kerr metric, focusing on scattering amplitudes, has been given by Nima Arkani-Hamed and collaborators. More broadly, the Kerr-Schild double copy is associated with a much larger story relating graviton and gluon amplitudes, known as the BCJ duality.